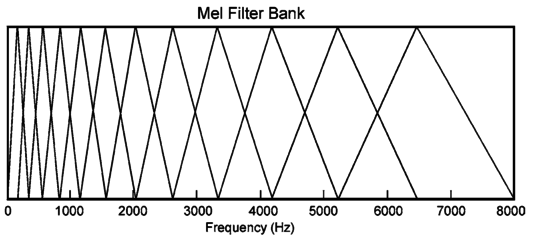
Contemporary music analysis with machine learning tools

Pablo E. Riera

Laboratorio de Acústica y Percepción Sonora y Laboratorio de Dinámica Sensomotora.

Universidad Nacional de Quilmes.


TALLER SOBRE APLICACIONES MATEMÁTICAS Y COMPUTACIONALES A LA MÚSICA
Buenos Aires - 14 al 18 de noviembre de 2016
Facultad de Ciencias Exactas y Naturales - Universidad de Buenos Aires
Convocado por el Centro Latinoamericano de Formación Interdisciplinaria (CELFI)

Contemporary Music, Electroacoustic Music and Experimental Music

“This listening experience is characterised by a new vision of time (i.e. atemporal, static, periodic), space (i.e. multi-channels diffusion and sculptural musical design), musical evolution (non-narrative and extended) and repetition (generation of hypnotic effects and a listening ‘in accumulation’). These characteristics form an (ec)static listening environment, where the musical material is static (atemporal, non-narrative) and the listening attitude is ecstatic (free to explore and move through the dimensions of sound).”

Wanke, R. (2015). A Cross-genre Study of the (Ec) Static Perspective of Today’s Music. Organised Sound, 20(03), 331-339.

Scope

  • Contemporary, electroacusctic and experimental music
  • Focus on timbre

Situation

  • How to compare timbres?
  • Different criteriums for grouping sound and making timbre spaces
  • Timbre spaces aren't unique

Attempts

  • For a specific musical piece, try to obtain a timbre space that allows to explore and go through the palette of sounds

Timbre spaces

Sounds of musical instruments may be positioned in a low dimensional space with dimensions asociated to acoustic attributes.

Grey, J. M. (1977). Multidimensional perceptual scaling of musical timbres. the Journal of the Acoustical Society of America, 61(5), 1270-1277

Analysis Procedure

Frames length of ~92 miliseconds with steps of ~23 miliseconds

Descriptors

Audio descriptors

  • MFCC (Mel Frequency Cepstrum Coefficients)
  • Chromagram
  • Spectral Centroid
  • Spectral Contrast

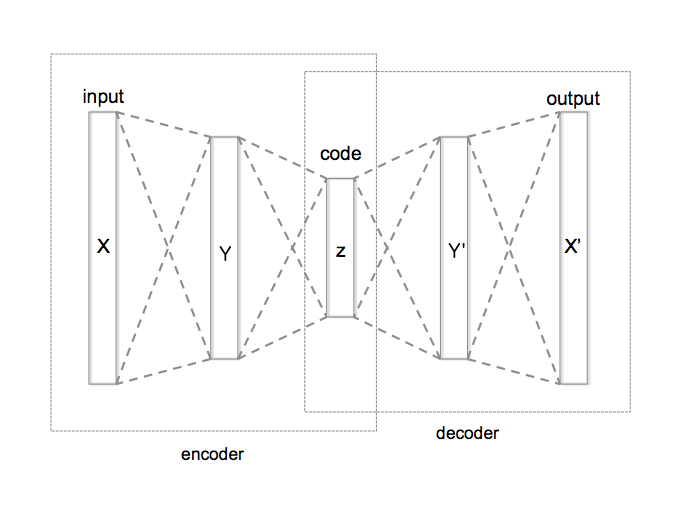
Unsupervised Learning with Autoencoders

  • Spectrum -> Encoding -> Low dimensional neuronal representation -> Decoding -> Spectrum

Analysis techniques

Machine learning

  • Reduction of dimensionality for timbre spaces construction
  • Clustering for grouping sounds

Visualization

  • Time evolution of position in timbre space

Sonification

  • Overlap and Add of fragments

MFCC

Mel Frequency Filter Bank

Discrete Cosine Transform basis

In [ ]:

Partiels (Grisey 1975)

In [36]:
%%HTML
<video width="640" height="640" controls>
  <source src="figs/Partiels/spectrogram_video.mp4" type="video/mp4">
</video>

Data normalization

Z Score

$ \huge \color{white}{ z={x-\mu \over \sigma } }$

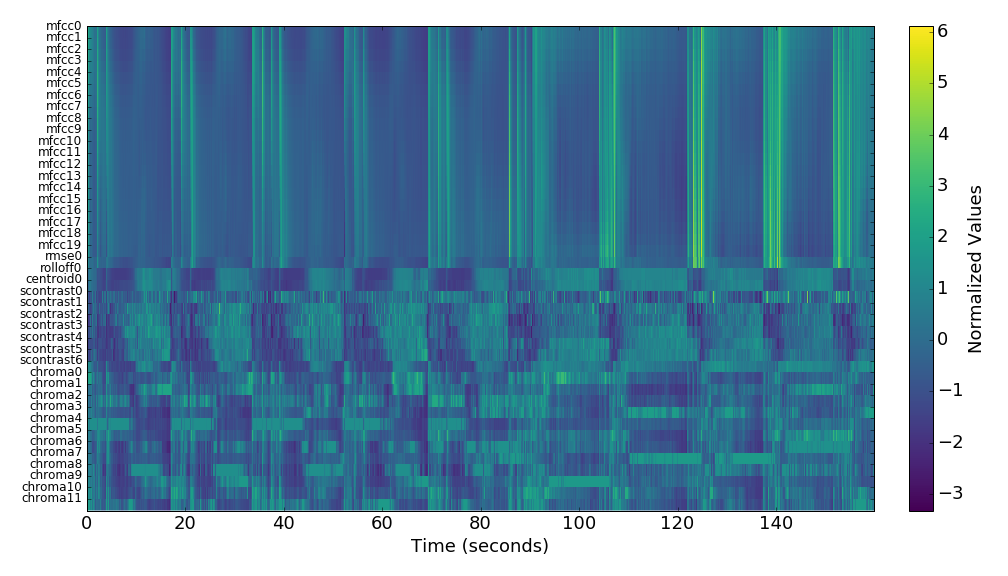
Features

Reduction of dimensionality

Principal component analysis

90% of variance yield 8 PC

In [37]:
%%HTML
<H1> Recurrence - Partiels Grisey (1975) </H1>
<video width="640" height="640" controls>
  <source src="figs/Partiels/recurrence_video.mp4" type="video/mp4">
</video>

Recurrence - Partiels Grisey (1975)

Dimensionality Reduction - Timbre Space

Multidimensional Scaling

In [39]:
%%HTML
<video width="640" height="480" controls>
  <source src="figs/Partiels/mds_video.mp4" type="video/mp4">
</video>

Clustering K - Means and Spectral

In [40]:
display(htmlimage(['figs/Partiels/mds_kmeans_labels.png'],512))
# ,'figs/Partiels/mds_spectral_labels.png'
# display(htmlimage('figs/Partiels/mds_kmeans_labels.png.png',512))

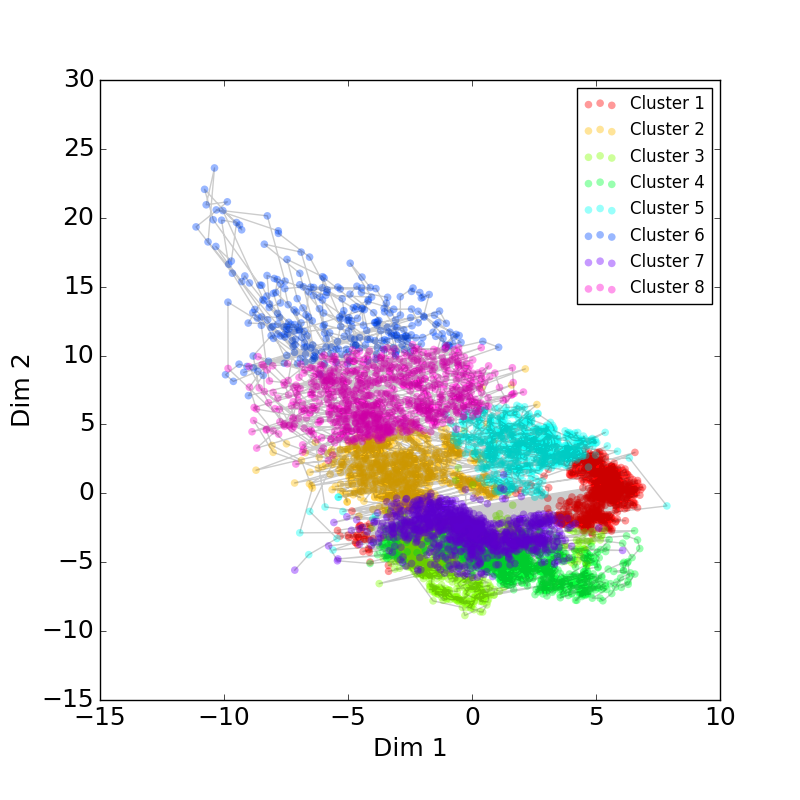
Clustering with K - Means

In [41]:
# import pickle
# sr = 44100
# with open('../mir/pickles/Partiels_data.pickle', 'rb') as handle:
#     s = pickle.load(handle)
    
# X = s['Xpca']
# n_clusters=X.shape[1]
# labels = s['kmeans_labels']
# print(s['name'])
# path = 'figs/'
# for i in range(n_clusters):
#     fname = s['name']+'/kmeans_cluster_'+str(i)+'.mp3'
#     display(audiofile(filename=path+fname))
path = 'figs/Partiels'
for i in range(8):
    fname = '/kmeans_cluster_'+str(i)+'.mp3'
    display(audiofile(filename=path+fname))

Following a path in timbre space

Wessel, D. L. (1979). Timbre space as a musical control structure. Computer music journal, 45-52.

Sorting the time axes with first principal component

In [44]:
display(audiofile(filename='figs/Partiels/pca_sorted.mp3'))

Traversing the recurrence graph

In [45]:
display(audiofile(filename='figs/Partiels/orderdfs.mp3'))

Timbre in the brain: Auditory cortical response

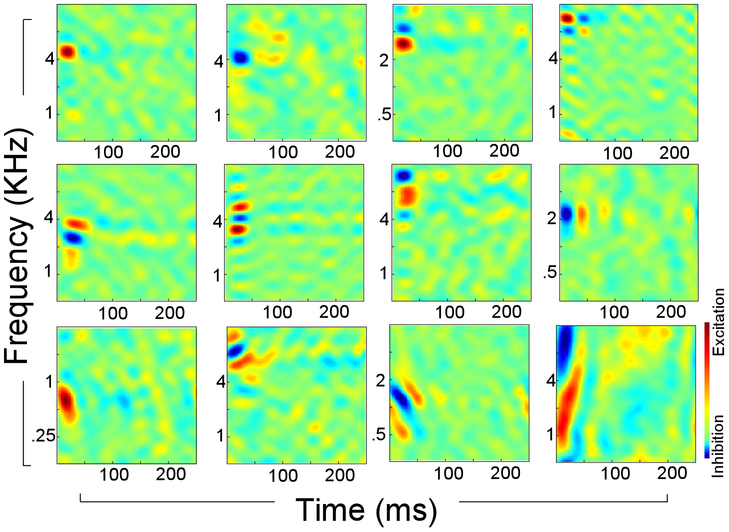Patil, K., Pressnitzer, D., Shamma, S., & Elhilali, M. (2012). Music in our ears: the biological bases of musical timbre perception. PLoS Comput Biol, 8(11)

Autoencoders

$$ \color{white}{ \mathbf{Y} = \tanh(\mathbf{W}\mathbf{X}+b) \\ \mathbf{X} = \tanh(\mathbf{W^T}\mathbf{Y}+b) }$$

Feed forward autoencoder

Encoder with 8 layers, activation function tanh and bias

Neurons per layers 1025, 768, 512, 256, 128, 64, 32, 16, 8

Data Dimensions: 6900 spectrums with 1025 frequency bins

Batch size 2000

In [46]:
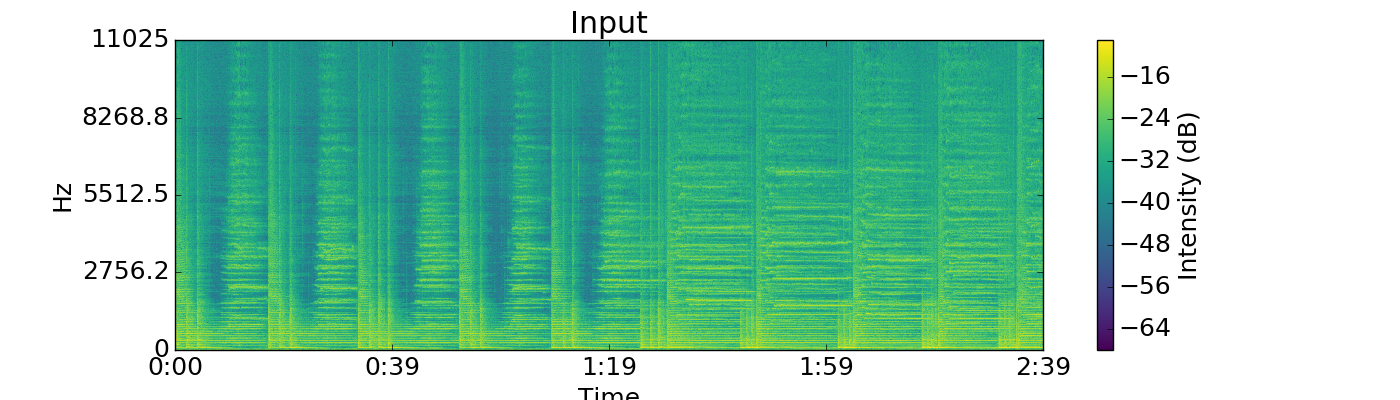
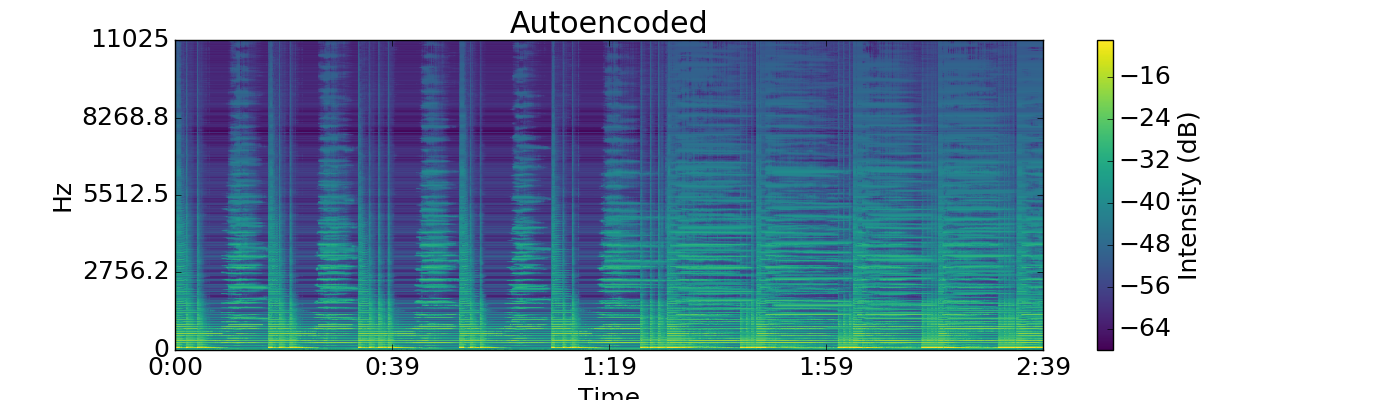
display(audiofile(filename='figs/Autoencoder/naeoutput_8.mp3'))

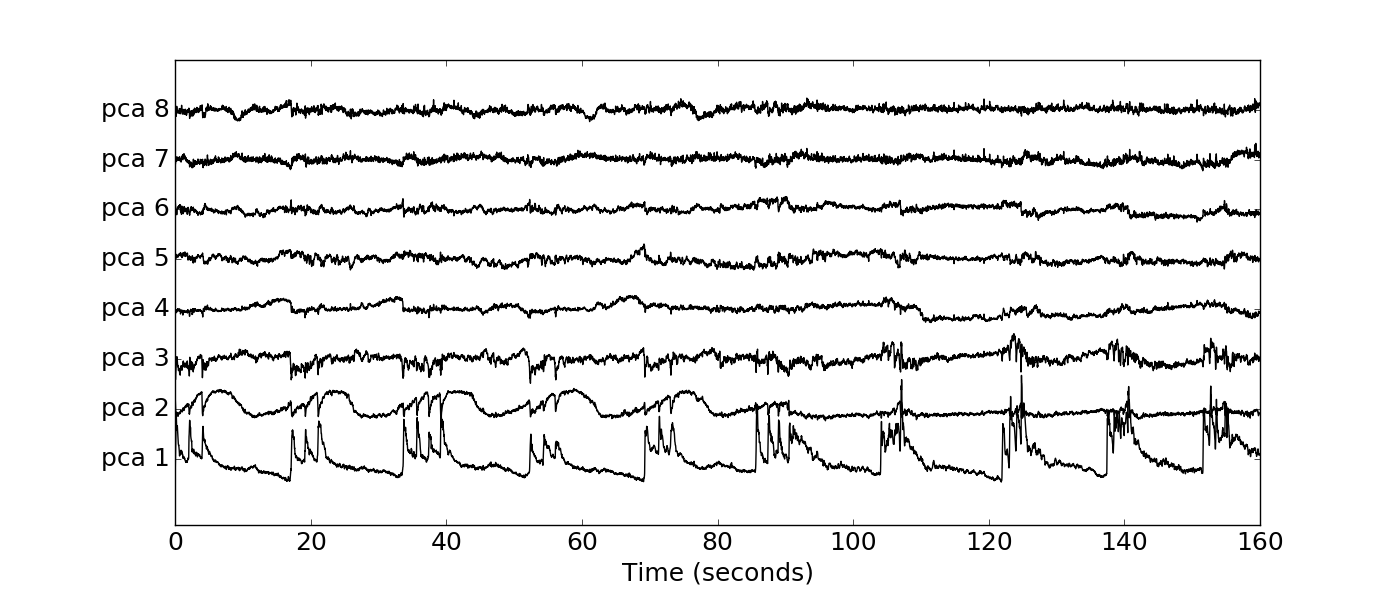
Code Layer Neuronal activity

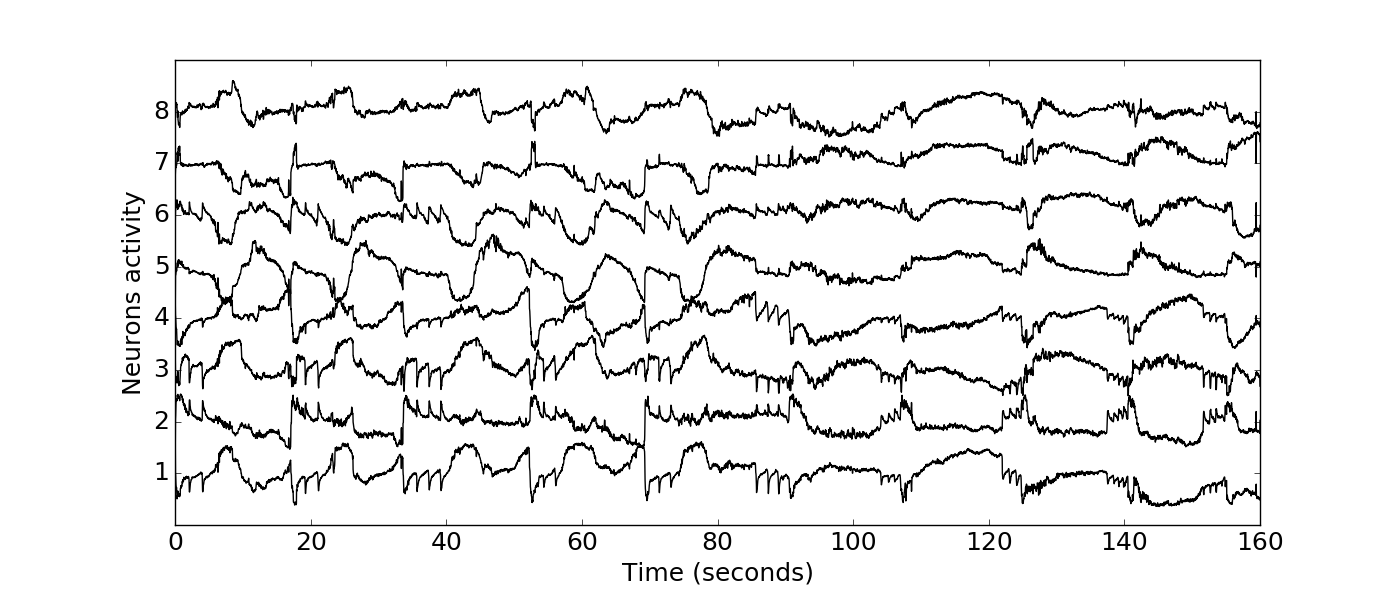
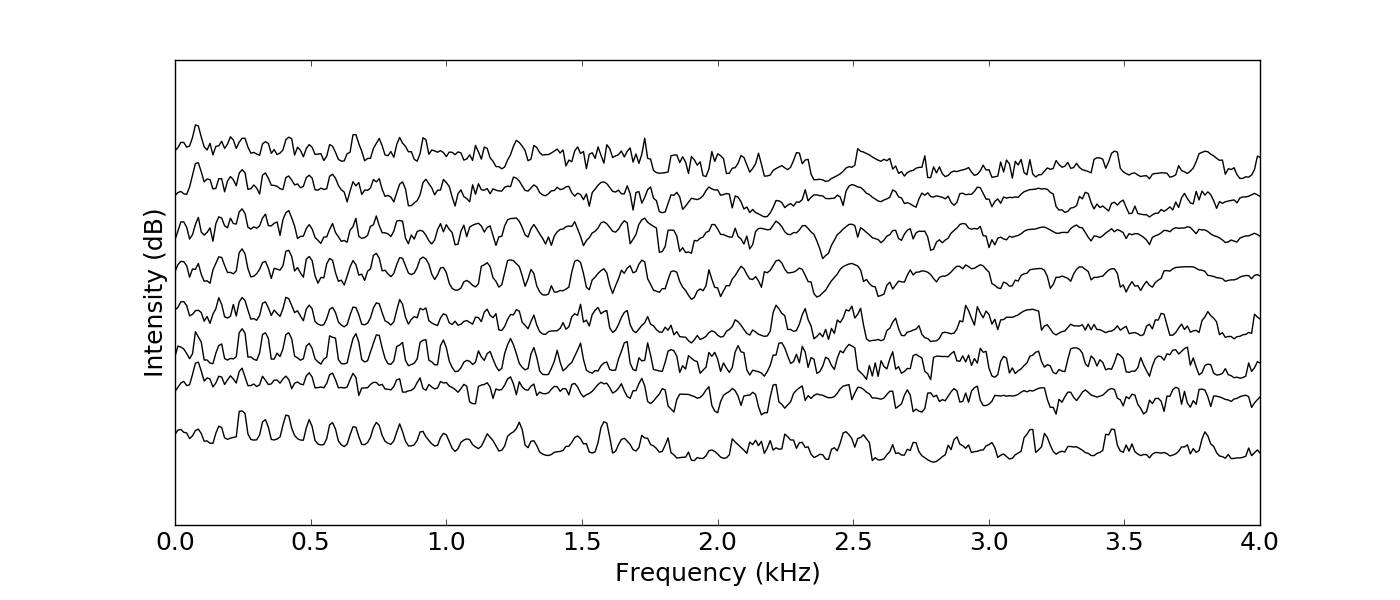
Spectral receptive fields in the encoded layer

In [47]:
display(audiofile(filename='figs/Autoencoder/zpath_8.mp3'))

Dimensionality Reduction - Timbre Space

Multidimensional Scaling

In [48]:
%%HTML
<video width="640" height="512" controls>
  <source src="figs/Partiels/mdsz_video.mp4" type="video/mp4">
</video>

Recurrence of neuronal activity

Cosine distance

In [49]:
display(htmlimage(['figs/Partiels_nae_inner_layer/recurrence_cosine.png'],512))

Conclusions

Audio Descriptors

  • Acceptable results for the two dimensional timbre space
  • Able to generate timbre organizations from clustering, PCA ordering and graph traversal

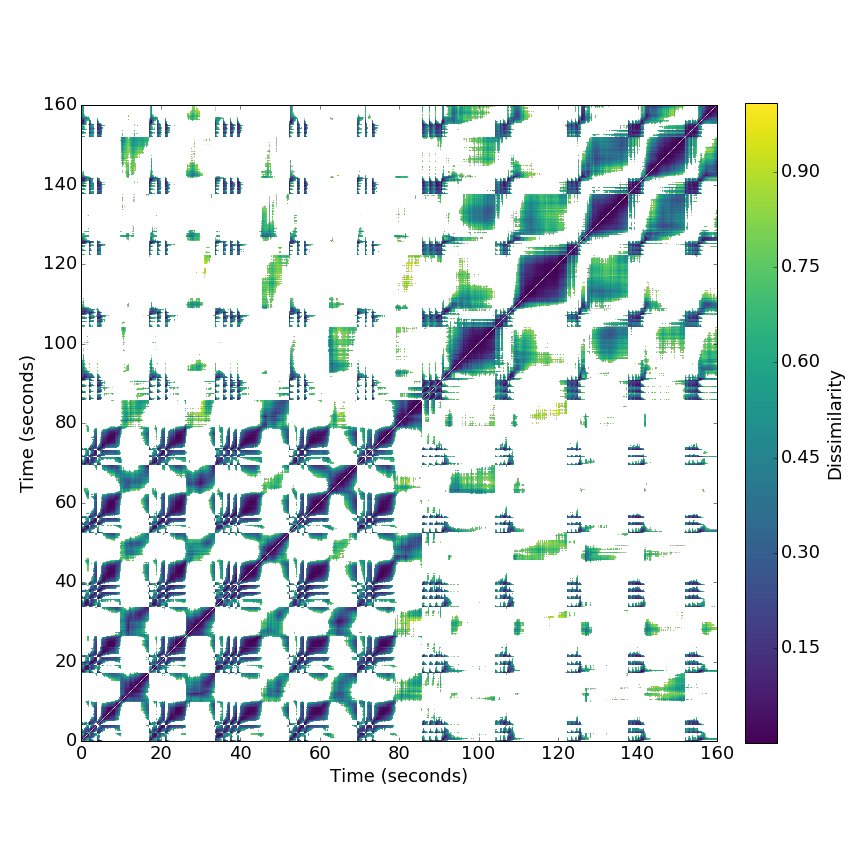
Autoencoder Neural activity

  • Autoencoder with 8 neurons bottleneck learns reasonably well because overfits the small dataset
  • Multidimensional scaling space is substantially different from Audio Descriptor results, but not acoustically correlated

Agradecimientos

  • Matias Zabaljauregui, Alejo Salles, Martín Miguel, Andrés Babino, Alma Laprida

Laboratorio de Dinámica Sensomotora UNQ http://ldsm.web.unq.edu.ar/

Laboratorio de Acústica y Percepción Sonora UNQ https://lapso.org

Laboratorio de Inteligencia Artificial Aplicada FCEyN UBA https://liaa.dc.uba.ar/